单因素方差分析
标签
学习/心理学
字数
1258 字
阅读时间
5 分钟
本章概览
t-检验和 z-检验不能用于多于2组的数据. 处理这类数据需要用 一种新的推论统计程序: 方差分析(ANOVA)。在方差分析中,我们利用F统计量来比较多组数据之间是否有显著差异。在统计显著性的基础上,我们又会应用两种事后检验方法比较两两之间的差异性,并对 ANOVA 的效应进行评估。
学习要点
- 区分单因素设计与因素设计
- 掌握ANOVA的逻辑
- 理解方差的可分解性
- 学会计算F统计值
- 掌握利用简便公式进行ANOVA的方法
- 学会进行事后检验
- 学会计算ANOVA的效应
单因素设计
在方差分析中,因素就是自变量。因此,只有一个自变量的研究被称为单因素设计。具有多个自变量的研究被称为多因素设计。构成因素的个别处理条件被称为因素的水平。
方差的分解
方差的可分解性
- 指总的离差平方和可以分解为几个不同来源的平方和。
总方差的组成
- 组间平方和(分子):处理间方差
- 组内平方和(分母):不是由于处理引起的方差
可简化为:
- 公式的理解:总平方和=组内平方和+组间平方和
F统计值
F=处理间均方/处理内均方
F分布
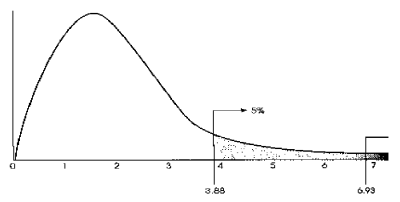
当F统计量的观测值小于临界值时,说明数据的总变异中,大部分是由实验误差和个体差异所致,不能认为实验处理有效;
当F统计量的观测值大于临界值时,说明实验数据的变异的确由不同的实验处理所造成,即不同处理之间存在差异。
使用F统计量的前提:1.总体正态;2.变异的同质性;3.独立性。
ANOVA的步骤
- 陈述原假设
和备择假设 ,确定进行检验的显著性水平 - 确定检验的方向性,需要注意的是 ANOVA 检验总是单尾检验
- 指出检验的自由度
,注意在 ANOVA 检验中有两个自由度,分别是组间变异的自由度 和组内变异的自由度 ,其中 为设置水平数, 为总的样本容量 - 根据组间自由度、组内自由度以及显著性水平
,查表找出临界 统计量的值 - 对于样本计算
统计量的值,画出如下图所示的方差分析表 
- 比较计算得出的
值和临界 值,如果 ,则接受原假设 ,如果 ,则拒绝 ,接受备择假设 - 进行事后检验。
事后检验
- ANOVA无法说明哪个备择假设得到支持;
- 要进行事后检验以说明各组差异在什么地方;
- 事后检验是比较每一个组和另一个处理组,一次比较两个,这称为成对比较。
族系误差
- 每一个比较都是一个单独的假设检验,每一个都有犯I类错误的风险。所以,比较对数越多,作结论的风险越大。即容易发现实际不存在的差异。这称为实验导致的
水平或族系误差; - 多次比较后犯 I 类错误的概率为
,其中c为比较的次数
Tukey's HSD 检验
- 此检验各组要有相同的样本容量;
- 可以计算出单一的值确定处理均值间的最小差异,考查此差异在统计上是否显著;
- q可以查表得到。
Scheffe检验 (Scheffe test)
- 适用于n不相等的情况;
- 降低I类错误的风险,提高II类错误的风险。
ANOVA的效应
效应大小与统计工具的敏感性无关,它表示几个总体平均值之间的距离,也不依赖样本容量这类测量特性。
效应量:
ANOVA 中 r 与效应量关系:
ANOVA中效应的评估:
| 效应的评估 | |
|---|---|
| 小的效应 | |
| 中等效应 | |
| 大的效应 |
 芷沐沐
芷沐沐